Wat is de wet van de grote getallen?
In de kansberekening is de wet van de grote getallen een theorie die het resultaat beschrijft van het een groot aantal keren uitvoeren van dezelfde test. Volgens de wet moet het gemiddelde van de resultaten van een groot aantal tests dicht bij de verwachte waarde liggen en heeft het de neiging steeds dichter bij de verwachte waarde te komen naarmate meer tests worden uitgevoerd.
De wet van de grote getallen is belangrijk omdat het stabiele langetermijnresultaten garandeert voor de gemiddelden van sommige willekeurige gebeurtenissen. Neem bijvoorbeeld een casino, terwijl een casino geld kan verliezen in één enkele draai van het roulettewiel, zullen de winsten neigen naar een voorspelbaar percentage over een groot aantal draaiingen. Elke winstreak van een speler zal uiteindelijk worden overwonnen door de parameters van het spel. Belangrijk is dat de wet alleen geldt wanneer een groot aantal waarnemingen in aanmerking worden genomen. Want iedereen kan wel is winnen door 1 keer in te zetten op rood of zwart, wanneer dit richting de 50 keer gaat wordt het steeds moeilijker om met geld thuis te komen.
Voorbeelden van de wet van de grote getallen
Om het nog iets duidelijker te maken is er ook een voorbeeld dat werkt aan de hand van dobbelstenen. Wanneer je met een dobbelsteen gooit heeft elke zijde evenveel kans om op te landen. Het gemiddelde van de dobbelstenen bij elkaar opgeteld is:
(1+2+3+4+5+6) / 6 = 3,5
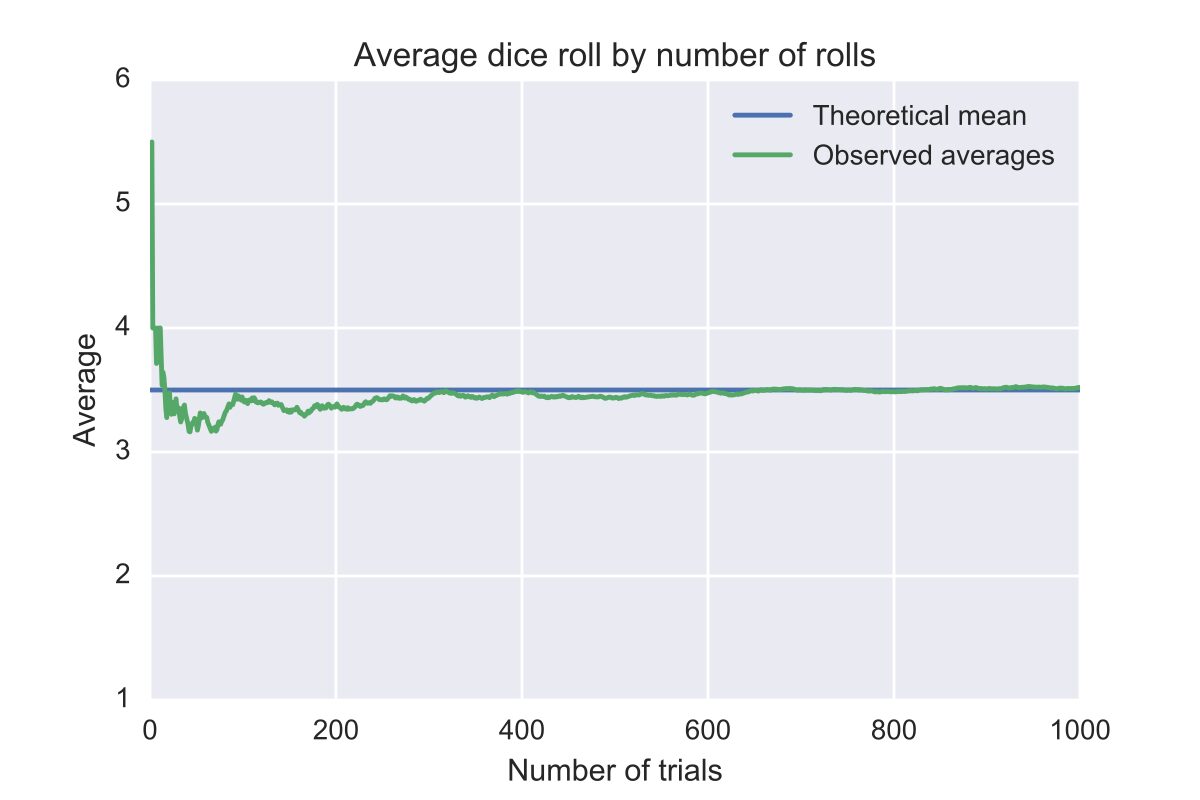
Stel je gooit 2 keer de dobbelsteen. Er is een kans dat je dan bijvoorbeeld 2 keer 6 gooit, of 1 keer 6 en 1 keer 5. Allebei ligt dit ver boven het gemiddelde van de dobbelsteen. Echter volgens de wet van de grote getallen betekent het dat hoe vaker je gooit des te dichter je bij de verwachte uitkomst van 3,5 komt. (Zie afbeelding). Bij de eerste 50 worpen fluctueert de uitkomst nog erg om het gemiddelde heen. Echter richting de 200 worpen komt de uitkomst steeds meer op het gemiddelde terecht.
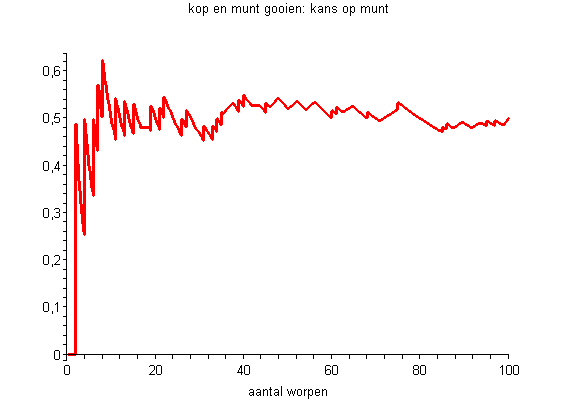
Hetzelfde geldt voor het gooien van een munt. Wanneer een eerlijke munt eenmaal wordt opgegooid, is de theoretische kans dat de uitkomst “kop” is gelijk aan 50%. Volgens de wet van de grote getallen moet de uitkomst dus 50% zijn wanneer er een groot aantal munten wordt gegooid. Op onderstaande afbeelding is wederom de uitkomst te zien van een groot aantal keer een munt opgooien.
De wet van de grote getallen in de commerciële wereld
De wet van de grote getallen kan ook gebruikt worden voor organisaties. Om als bedrijf zeker te weten of sommige beslissingen juist zijn kan je de wet van de grote getallen gebruiken. Ons brein heeft namelijk niet de capaciteit om altijd de logische beslissing te nemen.
Stel dat wij mensen een doos voor ons hebben waar we niet van weten wat er in zit. Iemand vertelt van tevoren dat wanneer je je hand in de doos steekt er een beloning (snoepje) of een straf (elektrische schok) in kan zitten. Stel je doet je hand in de doos en je krijgt een schok. Wij mensen denken dan niet: laat ik het nog een keer proberen om mijn hand in de doos te doen. Echter is het mogelijk dat na 100 keer proberen blijkt het dat je maar 5 keer een schok hebt gehad en 95 beloningen.
Dit betekent in de commerciële wereld vooral: maak niet te gehaaste beslissingen voordat je echt de uitkomst weet. Als je een A/B test uitvoert en je ziet dat er van de eerste 10 mensen, 8 op advertentie A klikken, kies dan niet gelijk voor advertentie A. Dit is een te kleine steekproef om een beslissing te nemen, kijk waar het uiteindelijke gemiddelde naar toe gaat en waar de lijn stabiliseert.
Hetzelfde geldt voor je CTR. Wanneer je ziet dat bijvoorbeeld een advertentie net online is en niemand er op klikt, stop dan niet gelijk met de advertentie. Wacht tot er een genoeg aantal vertoningen zijn om daadwerkelijk een juiste beslissing te kunnen nemen.